TL;DR
This project tests a cointegrated pairs trading strategy on the 40 largest Italian companies in the FTSE MIB, exploiting potential inefficiencies in a smaller market. The method uses OLS regression and the ADF test to identify cointegrated pairs with high correlation, applying a mean-reverting contrarian strategy based on Z-score thresholds (±2.25) for trade entries and exits. Backtests from 2017-2023 show strong performance: an overall return of 67.2% vs. 43.1% for the index, annual volatility of 4%, a Sharpe ratio of 2.05, and a max drawdown of - 3.07%.
The out-of-sample period performed even better, with a Sharpe ratio of 2.32 and a max drawdown of - 2.33%, confirming robustness. Results suggest the strategy is resilient, especially during volatile periods like COVID-19, and could be further improved by testing multiple entry levels, accounting for transaction costs, and experimenting with different parameter estimation ranges.
About the Author

Andrea Mangiucca is a finance professional and Trading Analyst at Morgan Stanley, with prior experience as a Fixed Income Trader Intern at Banca Investis S.p.A. He holds a Master’s in Finance (cum laude) and a Bachelor’s in Economics and Management from Luiss Guido Carli University, where his thesis focused on pair trading strategies.
A recipient of the EPAT® Certificate of Excellence from QuantInsti, Andrea has also excelled in global competitions, including the CME Group University Trading Challenge and the Rotman Trading Competition. Skilled in Python and quantitative finance, he is passionate about algorithmic strategy development, market analysis, and continuous learning. Beyond trading, he has contributed as a volunteer kickboxing instructor, reflecting his leadership and community engagement.
Project Idea and Motivation
My project topic is to test a Cointegrated pair trading strategy on the 40 most capitalised Italian companies of the FTSE MIB. The reason why I chose the Italian market is because I believe that in a smaller environment, there might be more inefficiencies to exploit and so, as a consequence, a more adjusted return, compared to a more developed market as the American. My motivation for choosing this approach is that I really like the idea and the model behind the strategy that I also studied in my university courses, and I believe that building a quantitative strategy on that particular topic could open doors to work in this environment once I finish my master's degree in finance.
The trading strategy implemented in this project is called “Statistical Arbitrage Trading”, also known as “Pairs Trading”. It is a contrarian strategy that aims to profit from the mean-reverting behaviour of a given pair ratio. The underlying assumption of this strategy is that the spread of pairs that exhibit characteristics of cointegration is inherently mean-reverting and therefore provides arbitrage opportunities when it deviates significantly from the mean.
The trading strategy is back-tested for the period between ‘07-01-2017’ and ’18-04-2023’. The period is divided into two-thirds for the in-sample back-test and the remaining third into an out-sample back-test.
Methodology Overview
My idea consists of the following steps:
Universe & Data:
We download from Yahoo Finance all the historical stock prices of the FTSE MIB index. Once cleaned and adjusted the dataset, removing, for example, the stocks with too many missing values, we generate all possible pairs of stocks.
Output:
[('A2A.MI', 'AMP.MI'),
('A2A.MI', 'AZM.MI'),
('A2A.MI', 'BGN.MI'),
('A2A.MI', 'BAMI.MI'),
('A2A.MI', 'BMED.MI'),
('A2A.MI', 'BPE.MI'),
('A2A.MI', 'BZU.MI'),
('A2A.MI', 'CPR.MI'),
('A2A.MI', 'CNHI.MI'),
('A2A.MI', 'DIA.MI'),
('A2A.MI', 'ENEL.MI'),
('A2A.MI', 'ENI.MI'),
('A2A.MI', 'RACE.MI'),
('A2A.MI', 'FBK.MI'),
('A2A.MI', 'G.MI'),
('A2A.MI', 'HER.MI'),
('A2A.MI', 'IP.MI'),
('A2A.MI', 'ISP.MI'),
('A2A.MI', 'INW.MI'),
('A2A.MI', 'IG.MI'),
('A2A.MI', 'LDO.MI'),
('A2A.MI', 'MB.MI'),
('A2A.MI', 'MONC.MI'),
('A2A.MI', 'PST.MI'),
('A2A.MI', 'PRY.MI'),
('A2A.MI', 'REC.MI'),
('A2A.MI', 'SPM.MI'),
('A2A.MI', 'SRG.MI'),
('A2A.MI', 'TIT.MI'),
('A2A.MI', 'TEN.MI'),
('A2A.MI', 'TRN.MI'),
('A2A.MI', 'UCG.MI'),
('A2A.MI', 'UNI.MI'),
('AMP.MI', 'AZM.MI'),
('AMP.MI', 'BGN.MI'),
('AMP.MI', 'BAMI.MI'),
('AMP.MI', 'BMED.MI'),
('AMP.MI', 'BPE.MI'),
('AMP.MI', 'BZU.MI'),
('AMP.MI', 'CPR.MI'),
('AMP.MI', 'CNHI.MI'),
('AMP.MI', 'DIA.MI'),
('AMP.MI', 'ENEL.MI'),
('AMP.MI', 'ENI.MI'),
('AMP.MI', 'RACE.MI'),
('AMP.MI', 'FBK.MI'),
('AMP.MI', 'G.MI'),
('AMP.MI', 'HER.MI'),
('AMP.MI', 'IP.MI'),
('AMP.MI', 'ISP.MI'),
('AMP.MI', 'INW.MI'),
('AMP.MI', 'IG.MI'),
('AMP.MI', 'LDO.MI'),
('AMP.MI', 'MB.MI'),
('AMP.MI', 'MONC.MI'),
('AMP.MI', 'PST.MI'),
('AMP.MI', 'PRY.MI'),
('AMP.MI', 'REC.MI'),
('AMP.MI', 'SPM.MI'),
('AMP.MI', 'SRG.MI'),
('AMP.MI', 'TIT.MI'),
('AMP.MI', 'TEN.MI'),
('AMP.MI', 'TRN.MI'),
('AMP.MI', 'UCG.MI'),
('AMP.MI', 'UNI.MI'),
('AZM.MI', 'BGN.MI'),
('AZM.MI', 'BAMI.MI'),
('AZM.MI', 'BMED.MI'),
('AZM.MI', 'BPE.MI'),
('AZM.MI', 'BZU.MI'),
('AZM.MI', 'CPR.MI'),
('AZM.MI', 'CNHI.MI'),
('AZM.MI', 'DIA.MI'),
('AZM.MI', 'ENEL.MI'),
('AZM.MI', 'ENI.MI'),
('AZM.MI', 'RACE.MI'),
('AZM.MI', 'FBK.MI'),
('AZM.MI', 'G.MI'),
('AZM.MI', 'HER.MI'),
('AZM.MI', 'IP.MI'),
('AZM.MI', 'ISP.MI'),
('AZM.MI', 'INW.MI'),
('AZM.MI', 'IG.MI'),
('AZM.MI', 'LDO.MI'),
('AZM.MI', 'MB.MI'),
('AZM.MI', 'MONC.MI'),
('AZM.MI', 'PST.MI'),
('AZM.MI', 'PRY.MI'),
('AZM.MI', 'REC.MI'),
('AZM.MI', 'SPM.MI'),
('AZM.MI', 'SRG.MI'),
('AZM.MI', 'TIT.MI'),
('AZM.MI', 'TEN.MI'),
('AZM.MI', 'TRN.MI'),
('AZM.MI', 'UCG.MI'),
('AZM.MI', 'UNI.MI'),
('BGN.MI', 'BAMI.MI'),
('BGN.MI', 'BMED.MI'),
('BGN.MI', 'BPE.MI'),
('BGN.MI', 'BZU.MI'),
('BGN.MI', 'CPR.MI'),
('BGN.MI', 'CNHI.MI'),
('BGN.MI', 'DIA.MI'),
('BGN.MI', 'ENEL.MI'),
('BGN.MI', 'ENI.MI'),
('BGN.MI', 'RACE.MI'),
('BGN.MI', 'FBK.MI'),
('BGN.MI', 'G.MI'),
('BGN.MI', 'HER.MI'),
('BGN.MI', 'IP.MI'),
('BGN.MI', 'ISP.MI'),
('BGN.MI', 'INW.MI'),
('BGN.MI', 'IG.MI'),
('BGN.MI', 'LDO.MI'),
('BGN.MI', 'MB.MI'),
('BGN.MI', 'MONC.MI'),
('BGN.MI', 'PST.MI'),
('BGN.MI', 'PRY.MI'),
('BGN.MI', 'REC.MI'),
('BGN.MI', 'SPM.MI'),
('BGN.MI', 'SRG.MI'),
('BGN.MI', 'TIT.MI'),
('BGN.MI', 'TEN.MI'),
('BGN.MI', 'TRN.MI'),
('BGN.MI', 'UCG.MI'),
('BGN.MI', 'UNI.MI'),
('BAMI.MI', 'BMED.MI'),
('BAMI.MI', 'BPE.MI'),
('BAMI.MI', 'BZU.MI'),
('BAMI.MI', 'CPR.MI'),
('BAMI.MI', 'CNHI.MI'),
('BAMI.MI', 'DIA.MI'),
('BAMI.MI', 'ENEL.MI'),
('BAMI.MI', 'ENI.MI'),
('BAMI.MI', 'RACE.MI'),
('BAMI.MI', 'FBK.MI'),
('BAMI.MI', 'G.MI'),
('BAMI.MI', 'HER.MI'),
('BAMI.MI', 'IP.MI'),
('BAMI.MI', 'ISP.MI'),
('BAMI.MI', 'INW.MI'),
('BAMI.MI', 'IG.MI'),
('BAMI.MI', 'LDO.MI'),
('BAMI.MI', 'MB.MI'),
('BAMI.MI', 'MONC.MI'),
('BAMI.MI', 'PST.MI'),
('BAMI.MI', 'PRY.MI'),
('BAMI.MI', 'REC.MI'),
('BAMI.MI', 'SPM.MI'),
('BAMI.MI', 'SRG.MI'),
('BAMI.MI', 'TIT.MI'),
('BAMI.MI', 'TEN.MI'),
('BAMI.MI', 'TRN.MI'),
('BAMI.MI', 'UCG.MI'),
('BAMI.MI', 'UNI.MI'),
('BMED.MI', 'BPE.MI'),
('BMED.MI', 'BZU.MI'),
('BMED.MI', 'CPR.MI'),
('BMED.MI', 'CNHI.MI'),
('BMED.MI', 'DIA.MI'),
('BMED.MI', 'ENEL.MI'),
('BMED.MI', 'ENI.MI'),
('BMED.MI', 'RACE.MI'),
('BMED.MI', 'FBK.MI'),
('BMED.MI', 'G.MI'),
('BMED.MI', 'HER.MI'),
('BMED.MI', 'IP.MI'),
('BMED.MI', 'ISP.MI'),
('BMED.MI', 'INW.MI'),
('BMED.MI', 'IG.MI'),
('BMED.MI', 'LDO.MI'),
('BMED.MI', 'MB.MI'),
('BMED.MI', 'MONC.MI'),
('BMED.MI', 'PST.MI'),
('BMED.MI', 'PRY.MI'),
('BMED.MI', 'REC.MI'),
('BMED.MI', 'SPM.MI'),
('BMED.MI', 'SRG.MI'),
('BMED.MI', 'TIT.MI'),
('BMED.MI', 'TEN.MI'),
('BMED.MI', 'TRN.MI'),
('BMED.MI', 'UCG.MI'),
('BMED.MI', 'UNI.MI'),
('BPE.MI', 'BZU.MI'),
('BPE.MI', 'CPR.MI'),
('BPE.MI', 'CNHI.MI'),
('BPE.MI', 'DIA.MI'),
('BPE.MI', 'ENEL.MI'),
('BPE.MI', 'ENI.MI'),
('BPE.MI', 'RACE.MI'),
('BPE.MI', 'FBK.MI'),
('BPE.MI', 'G.MI'),
('BPE.MI', 'HER.MI'),
('BPE.MI', 'IP.MI'),
('BPE.MI', 'ISP.MI'),
('BPE.MI', 'INW.MI'),
('BPE.MI', 'IG.MI'),
('BPE.MI', 'LDO.MI'),
('BPE.MI', 'MB.MI'),
('BPE.MI', 'MONC.MI'),
('BPE.MI', 'PST.MI'),
('BPE.MI', 'PRY.MI'),
('BPE.MI', 'REC.MI'),
('BPE.MI', 'SPM.MI'),
('BPE.MI', 'SRG.MI'),
('BPE.MI', 'TIT.MI'),
('BPE.MI', 'TEN.MI'),
('BPE.MI', 'TRN.MI'),
('BPE.MI', 'UCG.MI'),
('BPE.MI', 'UNI.MI'),
('BZU.MI', 'CPR.MI'),
('BZU.MI', 'CNHI.MI'),
('BZU.MI', 'DIA.MI'),
('BZU.MI', 'ENEL.MI'),
('BZU.MI', 'ENI.MI'),
('BZU.MI', 'RACE.MI'),
('BZU.MI', 'FBK.MI'),
('BZU.MI', 'G.MI'),
('BZU.MI', 'HER.MI'),
('BZU.MI', 'IP.MI'),
('BZU.MI', 'ISP.MI'),
('BZU.MI', 'INW.MI'),
('BZU.MI', 'IG.MI'),
('BZU.MI', 'LDO.MI'),
('BZU.MI', 'MB.MI'),
('BZU.MI', 'MONC.MI'),
('BZU.MI', 'PST.MI'),
('BZU.MI', 'PRY.MI'),
('BZU.MI', 'REC.MI'),
('BZU.MI', 'SPM.MI'),
('BZU.MI', 'SRG.MI'),
('BZU.MI', 'TIT.MI'),
('BZU.MI', 'TEN.MI'),
('BZU.MI', 'TRN.MI'),
('BZU.MI', 'UCG.MI'),
('BZU.MI', 'UNI.MI'),
('CPR.MI', 'CNHI.MI'),
('CPR.MI', 'DIA.MI'),
('CPR.MI', 'ENEL.MI'),
('CPR.MI', 'ENI.MI'),
('CPR.MI', 'RACE.MI'),
('CPR.MI', 'FBK.MI'),
('CPR.MI', 'G.MI'),
('CPR.MI', 'HER.MI'),
('CPR.MI', 'IP.MI'),
('CPR.MI', 'ISP.MI'),
('CPR.MI', 'INW.MI'),
('CPR.MI', 'IG.MI'),
('CPR.MI', 'LDO.MI'),
('CPR.MI', 'MB.MI'),
('CPR.MI', 'MONC.MI'),
('CPR.MI', 'PST.MI'),
('CPR.MI', 'PRY.MI'),
('CPR.MI', 'REC.MI'),
('CPR.MI', 'SPM.MI'),
('CPR.MI', 'SRG.MI'),
('CPR.MI', 'TIT.MI'),
('CPR.MI', 'TEN.MI'),
('CPR.MI', 'TRN.MI'),
('CPR.MI', 'UCG.MI'),
('CPR.MI', 'UNI.MI'),
('CNHI.MI', 'DIA.MI'),
('CNHI.MI', 'ENEL.MI'),
('CNHI.MI', 'ENI.MI'),
('CNHI.MI', 'RACE.MI'),
('CNHI.MI', 'FBK.MI'),
('CNHI.MI', 'G.MI'),
('CNHI.MI', 'HER.MI'),
('CNHI.MI', 'IP.MI'),
('CNHI.MI', 'ISP.MI'),
('CNHI.MI', 'INW.MI'),
('CNHI.MI', 'IG.MI'),
('CNHI.MI', 'LDO.MI'),
('CNHI.MI', 'MB.MI'),
('CNHI.MI', 'MONC.MI'),
('CNHI.MI', 'PST.MI'),
('CNHI.MI', 'PRY.MI'),
('CNHI.MI', 'REC.MI'),
('CNHI.MI', 'SPM.MI'),
('CNHI.MI', 'SRG.MI'),
('CNHI.MI', 'TIT.MI'),
('CNHI.MI', 'TEN.MI'),
('CNHI.MI', 'TRN.MI'),
('CNHI.MI', 'UCG.MI'),
('CNHI.MI', 'UNI.MI'),
('DIA.MI', 'ENEL.MI'),
('DIA.MI', 'ENI.MI'),
('DIA.MI', 'RACE.MI'),
('DIA.MI', 'FBK.MI'),
('DIA.MI', 'G.MI'),
('DIA.MI', 'HER.MI'),
('DIA.MI', 'IP.MI'),
('DIA.MI', 'ISP.MI'),
('DIA.MI', 'INW.MI'),
('DIA.MI', 'IG.MI'),
('DIA.MI', 'LDO.MI'),
('DIA.MI', 'MB.MI'),
('DIA.MI', 'MONC.MI'),
('DIA.MI', 'PST.MI'),
('DIA.MI', 'PRY.MI'),
('DIA.MI', 'REC.MI'),
('DIA.MI', 'SPM.MI'),
('DIA.MI', 'SRG.MI'),
('DIA.MI', 'TIT.MI'),
('DIA.MI', 'TEN.MI'),
('DIA.MI', 'TRN.MI'),
('DIA.MI', 'UCG.MI'),
('DIA.MI', 'UNI.MI'),
('ENEL.MI', 'ENI.MI'),
('ENEL.MI', 'RACE.MI'),
('ENEL.MI', 'FBK.MI'),
('ENEL.MI', 'G.MI'),
('ENEL.MI', 'HER.MI'),
('ENEL.MI', 'IP.MI'),
('ENEL.MI', 'ISP.MI'),
('ENEL.MI', 'INW.MI'),
('ENEL.MI', 'IG.MI'),
('ENEL.MI', 'LDO.MI'),
('ENEL.MI', 'MB.MI'),
('ENEL.MI', 'MONC.MI'),
('ENEL.MI', 'PST.MI'),
('ENEL.MI', 'PRY.MI'),
('ENEL.MI', 'REC.MI'),
('ENEL.MI', 'SPM.MI'),
('ENEL.MI', 'SRG.MI'),
('ENEL.MI', 'TIT.MI'),
('ENEL.MI', 'TEN.MI'),
('ENEL.MI', 'TRN.MI'),
('ENEL.MI', 'UCG.MI'),
('ENEL.MI', 'UNI.MI'),
('ENI.MI', 'RACE.MI'),
('ENI.MI', 'FBK.MI'),
('ENI.MI', 'G.MI'),
('ENI.MI', 'HER.MI'),
('ENI.MI', 'IP.MI'),
('ENI.MI', 'ISP.MI'),
('ENI.MI', 'INW.MI'),
('ENI.MI', 'IG.MI'),
('ENI.MI', 'LDO.MI'),
('ENI.MI', 'MB.MI'),
('ENI.MI', 'MONC.MI'),
('ENI.MI', 'PST.MI'),
('ENI.MI', 'PRY.MI'),
('ENI.MI', 'REC.MI'),
('ENI.MI', 'SPM.MI'),
('ENI.MI', 'SRG.MI'),
('ENI.MI', 'TIT.MI'),
('ENI.MI', 'TEN.MI'),
('ENI.MI', 'TRN.MI'),
('ENI.MI', 'UCG.MI'),
('ENI.MI', 'UNI.MI'),
('RACE.MI', 'FBK.MI'),
('RACE.MI', 'G.MI'),
('RACE.MI', 'HER.MI'),
('RACE.MI', 'IP.MI'),
('RACE.MI', 'ISP.MI'),
('RACE.MI', 'INW.MI'),
('RACE.MI', 'IG.MI'),
('RACE.MI', 'LDO.MI'),
('RACE.MI', 'MB.MI'),
('RACE.MI', 'MONC.MI'),
('RACE.MI', 'PST.MI'),
('RACE.MI', 'PRY.MI'),
('RACE.MI', 'REC.MI'),
('RACE.MI', 'SPM.MI'),
('RACE.MI', 'SRG.MI'),
('RACE.MI', 'TIT.MI'),
('RACE.MI', 'TEN.MI'),
('RACE.MI', 'TRN.MI'),
('RACE.MI', 'UCG.MI'),
('RACE.MI', 'UNI.MI'),
('FBK.MI', 'G.MI'),
('FBK.MI', 'HER.MI'),
('FBK.MI', 'IP.MI'),
('FBK.MI', 'ISP.MI'),
('FBK.MI', 'INW.MI'),
('FBK.MI', 'IG.MI'),
('FBK.MI', 'LDO.MI'),
('FBK.MI', 'MB.MI'),
('FBK.MI', 'MONC.MI'),
('FBK.MI', 'PST.MI'),
('FBK.MI', 'PRY.MI'),
('FBK.MI', 'REC.MI'),
('FBK.MI', 'SPM.MI'),
('FBK.MI', 'SRG.MI'),
('FBK.MI', 'TIT.MI'),
('FBK.MI', 'TEN.MI'),
('FBK.MI', 'TRN.MI'),
('FBK.MI', 'UCG.MI'),
('FBK.MI', 'UNI.MI'),
('G.MI', 'HER.MI'),
('G.MI', 'IP.MI'),
('G.MI', 'ISP.MI'),
('G.MI', 'INW.MI'),
('G.MI', 'IG.MI'),
('G.MI', 'LDO.MI'),
('G.MI', 'MB.MI'),
('G.MI', 'MONC.MI'),
('G.MI', 'PST.MI'),
('G.MI', 'PRY.MI'),
('G.MI', 'REC.MI'),
('G.MI', 'SPM.MI'),
('G.MI', 'SRG.MI'),
('G.MI', 'TIT.MI'),
('G.MI', 'TEN.MI'),
('G.MI', 'TRN.MI'),
('G.MI', 'UCG.MI'),
('G.MI', 'UNI.MI'),
('HER.MI', 'IP.MI'),
('HER.MI', 'ISP.MI'),
('HER.MI', 'INW.MI'),
('HER.MI', 'IG.MI'),
('HER.MI', 'LDO.MI'),
('HER.MI', 'MB.MI'),
('HER.MI', 'MONC.MI'),
('HER.MI', 'PST.MI'),
('HER.MI', 'PRY.MI'),
('HER.MI', 'REC.MI'),
('HER.MI', 'SPM.MI'),
('HER.MI', 'SRG.MI'),
('HER.MI', 'TIT.MI'),
('HER.MI', 'TEN.MI'),
('HER.MI', 'TRN.MI'),
('HER.MI', 'UCG.MI'),
('HER.MI', 'UNI.MI'),
('IP.MI', 'ISP.MI'),
('IP.MI', 'INW.MI'),
('IP.MI', 'IG.MI'),
('IP.MI', 'LDO.MI'),
('IP.MI', 'MB.MI'),
('IP.MI', 'MONC.MI'),
('IP.MI', 'PST.MI'),
('IP.MI', 'PRY.MI'),
('IP.MI', 'REC.MI'),
('IP.MI', 'SPM.MI'),
('IP.MI', 'SRG.MI'),
('IP.MI', 'TIT.MI'),
('IP.MI', 'TEN.MI'),
('IP.MI', 'TRN.MI'),
('IP.MI', 'UCG.MI'),
('IP.MI', 'UNI.MI'),
('ISP.MI', 'INW.MI'),
('ISP.MI', 'IG.MI'),
('ISP.MI', 'LDO.MI'),
('ISP.MI', 'MB.MI'),
('ISP.MI', 'MONC.MI'),
('ISP.MI', 'PST.MI'),
('ISP.MI', 'PRY.MI'),
('ISP.MI', 'REC.MI'),
('ISP.MI', 'SPM.MI'),
('ISP.MI', 'SRG.MI'),
('ISP.MI', 'TIT.MI'),
('ISP.MI', 'TEN.MI'),
('ISP.MI', 'TRN.MI'),
('ISP.MI', 'UCG.MI'),
('ISP.MI', 'UNI.MI'),
('INW.MI', 'IG.MI'),
('INW.MI', 'LDO.MI'),
('INW.MI', 'MB.MI'),
('INW.MI', 'MONC.MI'),
('INW.MI', 'PST.MI'),
('INW.MI', 'PRY.MI'),
('INW.MI', 'REC.MI'),
('INW.MI', 'SPM.MI'),
('INW.MI', 'SRG.MI'),
('INW.MI', 'TIT.MI'),
('INW.MI', 'TEN.MI'),
('INW.MI', 'TRN.MI'),
('INW.MI', 'UCG.MI'),
('INW.MI', 'UNI.MI'),
('IG.MI', 'LDO.MI'),
('IG.MI', 'MB.MI'),
('IG.MI', 'MONC.MI'),
('IG.MI', 'PST.MI'),
('IG.MI', 'PRY.MI'),
('IG.MI', 'REC.MI'),
('IG.MI', 'SPM.MI'),
('IG.MI', 'SRG.MI'),
('IG.MI', 'TIT.MI'),
('IG.MI', 'TEN.MI'),
('IG.MI', 'TRN.MI'),
('IG.MI', 'UCG.MI'),
('IG.MI', 'UNI.MI'),
('LDO.MI', 'MB.MI'),
('LDO.MI', 'MONC.MI'),
('LDO.MI', 'PST.MI'),
('LDO.MI', 'PRY.MI'),
('LDO.MI', 'REC.MI'),
('LDO.MI', 'SPM.MI'),
('LDO.MI', 'SRG.MI'),
('LDO.MI', 'TIT.MI'),
('LDO.MI', 'TEN.MI'),
('LDO.MI', 'TRN.MI'),
('LDO.MI', 'UCG.MI'),
('LDO.MI', 'UNI.MI'),
('MB.MI', 'MONC.MI'),
('MB.MI', 'PST.MI'),
('MB.MI', 'PRY.MI'),
('MB.MI', 'REC.MI'),
('MB.MI', 'SPM.MI'),
('MB.MI', 'SRG.MI'),
('MB.MI', 'TIT.MI'),
('MB.MI', 'TEN.MI'),
('MB.MI', 'TRN.MI'),
('MB.MI', 'UCG.MI'),
('MB.MI', 'UNI.MI'),
('MONC.MI', 'PST.MI'),
('MONC.MI', 'PRY.MI'),
('MONC.MI', 'REC.MI'),
('MONC.MI', 'SPM.MI'),
('MONC.MI', 'SRG.MI'),
('MONC.MI', 'TIT.MI'),
('MONC.MI', 'TEN.MI'),
('MONC.MI', 'TRN.MI'),
('MONC.MI', 'UCG.MI'),
('MONC.MI', 'UNI.MI'),
('PST.MI', 'PRY.MI'),
('PST.MI', 'REC.MI'),
('PST.MI', 'SPM.MI'),
('PST.MI', 'SRG.MI'),
('PST.MI', 'TIT.MI'),
('PST.MI', 'TEN.MI'),
('PST.MI', 'TRN.MI'),
('PST.MI', 'UCG.MI'),
('PST.MI', 'UNI.MI'),
('PRY.MI', 'REC.MI'),
('PRY.MI', 'SPM.MI'),
('PRY.MI', 'SRG.MI'),
('PRY.MI', 'TIT.MI'),
('PRY.MI', 'TEN.MI'),
('PRY.MI', 'TRN.MI'),
('PRY.MI', 'UCG.MI'),
('PRY.MI', 'UNI.MI'),
('REC.MI', 'SPM.MI'),
('REC.MI', 'SRG.MI'),
('REC.MI', 'TIT.MI'),
('REC.MI', 'TEN.MI'),
('REC.MI', 'TRN.MI'),
('REC.MI', 'UCG.MI'),
('REC.MI', 'UNI.MI'),
('SPM.MI', 'SRG.MI'),
('SPM.MI', 'TIT.MI'),
('SPM.MI', 'TEN.MI'),
('SPM.MI', 'TRN.MI'),
('SPM.MI', 'UCG.MI'),
('SPM.MI', 'UNI.MI'),
('SRG.MI', 'TIT.MI'),
('SRG.MI', 'TEN.MI'),
('SRG.MI', 'TRN.MI'),
('SRG.MI', 'UCG.MI'),
('SRG.MI', 'UNI.MI'),
('TIT.MI', 'TEN.MI'),
('TIT.MI', 'TRN.MI'),
('TIT.MI', 'UCG.MI'),
('TIT.MI', 'UNI.MI'),
('TEN.MI', 'TRN.MI'),
('TEN.MI', 'UCG.MI'),
('TEN.MI', 'UNI.MI'),
('TRN.MI', 'UCG.MI'),
('TRN.MI', 'UNI.MI'),
('UCG.MI', 'UNI.MI')]Spread Construction & Parameter Estimation:
The spreads to trade are generated by Beta coefficients, estimated by running an OLS regressor for each pair. It is important to say that the parameters are estimated only for the first two-thirds of the total period; in this way, we can obtain more reliable results in the out-of-sample period.
Beta Coefficient (A2A.MI, AMP.MI) 0.053863 (A2A.MI, AZM.MI) 0.092766 (A2A.MI, BGN.MI) 0.058641 (A2A.MI, BAMI.MI) 0.599397 (A2A.MI, BMED.MI) 0.236300 ... ... (TEN.MI, UCG.MI) 0.927730 (TEN.MI, UNI.MI) 2.995193 (TRN.MI, UCG.MI) 0.411557 (TRN.MI, UNI.MI) 1.465156 (UCG.MI, UNI.MI) 3.219330 561 rows × 1 columns
Stationarity & Pair Selection:
The next step consists of performing an ADF Test to check stationarity, since we want only mean-reverting spreads. We only pick those with resulting values < -2.862… (cointegrated at 95% confidence level). These are the pairs, and consequently the selected spreads, to which we will apply the strategy. Note that all pairs have a correlation > 0.8.
the number of elegibile stocks are: 19
adf results cointegrated
(A2A.MI, MB.MI) -2.954400 True
(AZM.MI, BGN.MI) -3.551783 True
(AZM.MI, BMED.MI) -3.315120 True
(BGN.MI, BMED.MI) -3.389598 True
(BMED.MI, PRY.MI) -2.961954 True
(BMED.MI, TRN.MI) -2.974511 True
(CPR.MI, FBK.MI) -3.199470 True
(CPR.MI, PST.MI) -3.085488 True
(CPR.MI, SRG.MI) -2.933102 True
(CPR.MI, UNI.MI) -2.875924 True
(RACE.MI, INW.MI) -3.645589 True
(FBK.MI, MONC.MI) -3.175017 True
(G.MI, UNI.MI) -4.594855 True
(IP.MI, MONC.MI) -2.979790 True
(INW.MI, TRN.MI) -3.164000 True
(IG.MI, SRG.MI) -3.029030 True
(IG.MI, UNI.MI) -3.413933 True
(MB.MI, UNI.MI) -3.223164 True
(SRG.MI, UNI.MI) -3.610605 TrueSignal Design (Z-Score):
Once the pairs have been selected, we can create a Z-score of the spreads involved. The +2.25 and -2.25 standard deviation levels that are shown in the graphs of 5 of the 19 spreads represent the market entry trigger levels.
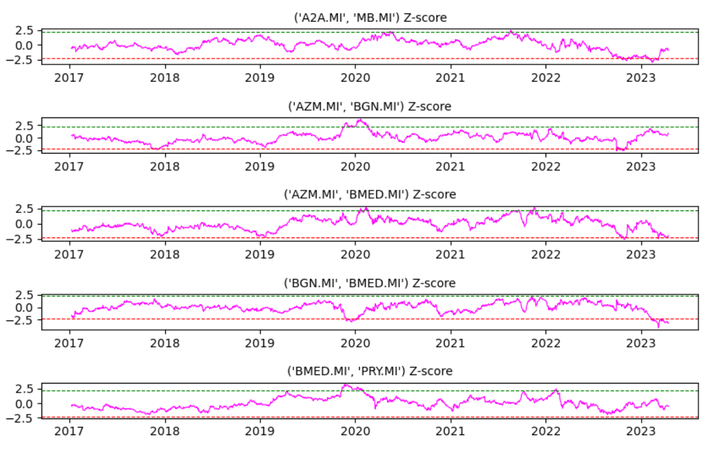
Execution Rules:
The trading strategy consists of going long when the spreads reach -2.25 std levels (buying X shares of the first company and selling X*Beta shares of the second) and doing the opposite operation when the spread exceeds the +2.25 std levels. The take profit is set at 0 value of std. During the back-test period, the stop loss will never be executed, since the pairs are cointegrated, but in a real situation, it is essential to use it.
Results
Pair-Level Illustrations:
These graphs show the returns of some single couples.
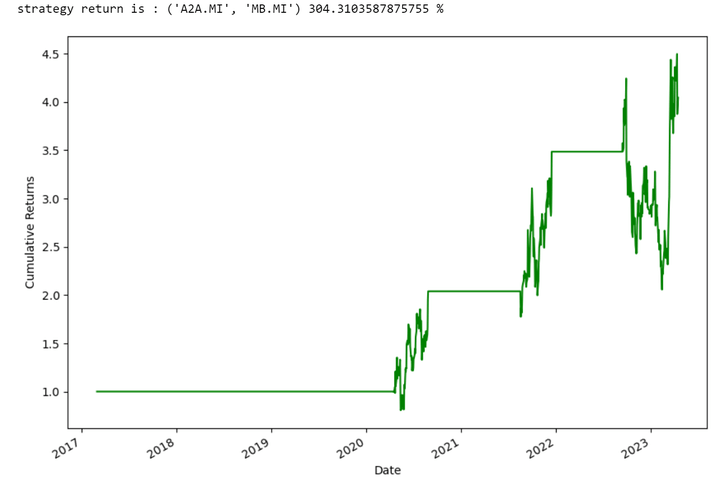
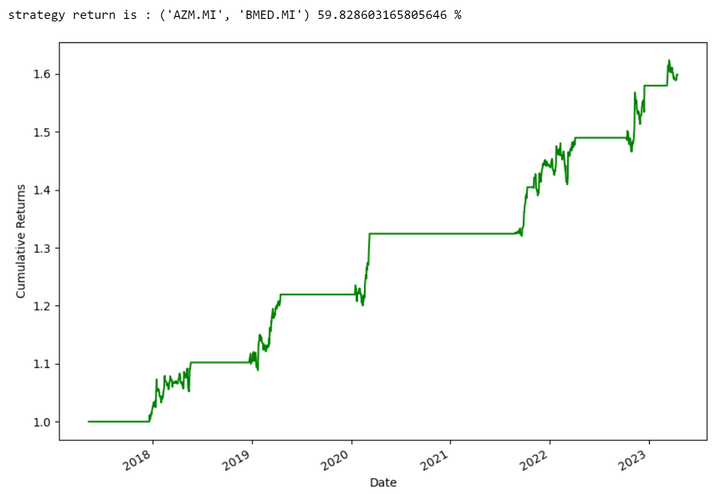
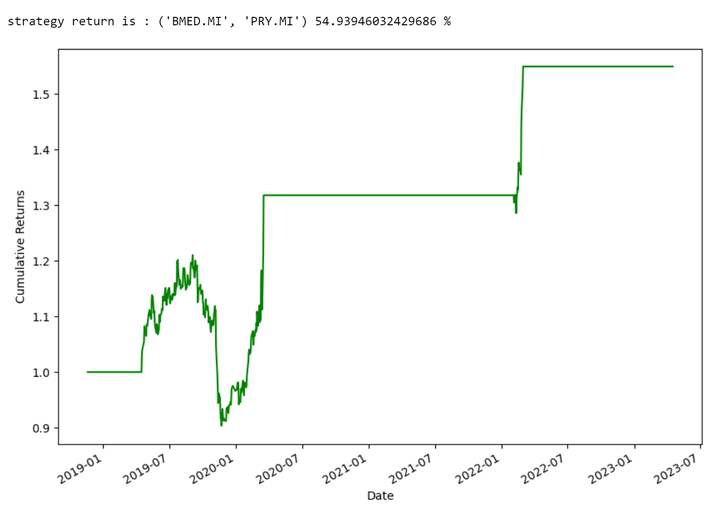
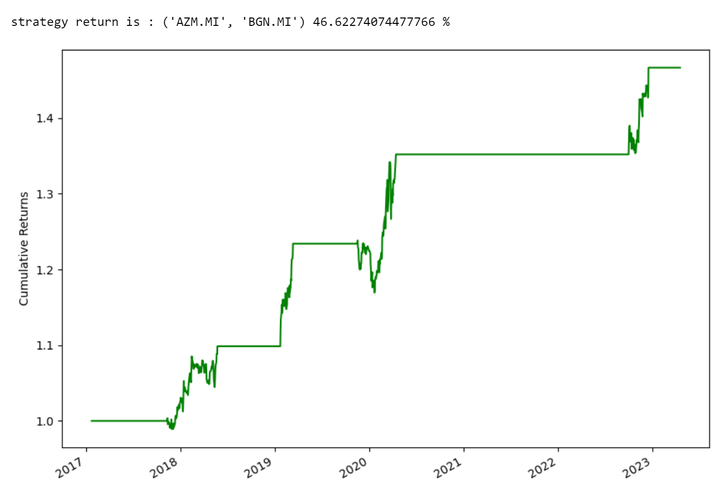
Output:
the total return of my portfolio is: 67.20561162079075 %
Output:
the total return of the Italian Stock Index is: 43.078512396694805 %
Output:
the In-Sample return of my portfolio is: 36.8908208468381 %
Output:
the Out-Sample return of my portfolio is: 22.145232665286095 %
Portfolio Construction:
We assume that every pair receives the same initial risk capital allocation, and then we compute the overall portfolio return. For example, assuming an initial capital of 10,000 $, we will invest 10.000/19 = 526.31 $ for each pair. The graph shows the return of the strategy compared with the performance of the benchmark. As we can see, the strategy return is higher, but the level of standard deviation is decidedly lower, and this will bring a much higher Sharpe ratio.
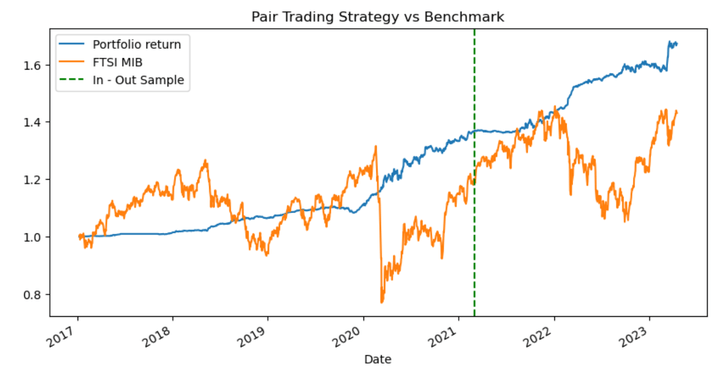
Performance (2017–2023, Full Sample)
Looking at the performance of the statistical-arbitrage strategy, we have an overall Return of 67.205% (compared with the 43.07% of the Index). The level of Volatility (ann.) is equal to 4.00%, this brings a good level of Sharpe Ratio of 2.05 and an optimal Max Drawdown (maximum loss) of -3.07%. The Longest Drawdown amounts to 147 days, but the Daily Value-at-Risk results equal -0.38%, which is a discrete outcome. All these performances suggest a possible use of financial leverage to improve the return.
Drawdowns & COVID-19 Regime
In this graph, we can observe the 5 worst drawdowns during the overall trading period. We can notice that the higher drawdown happens from April to June 2020, probably due to a significant increase in volatility given by the outbreak of the COVID pandemic. It is curious to note that after the worst drawdown, the strategist started to perform much better than in the past. This is probably because, as empirically demonstrated, during periods of crisis, the correlation between stocks increases.
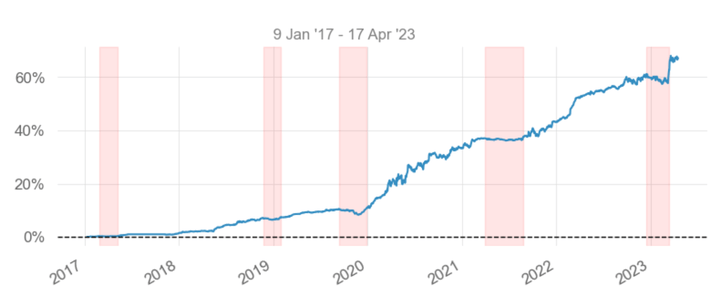
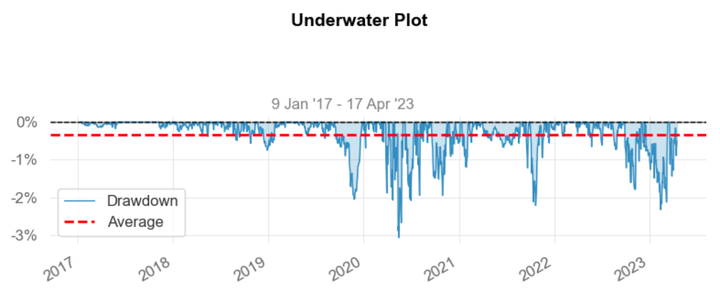
Return Distribution
As it is possible to see, the distribution of the Monthly Returns differs from the Gaussian one; in fact, it presents a positive skew and a kurtosis value greater than 0. This implies that the distribution has heavier tails and a sharper peak compared to a normal distribution. In other words, it indicates that there are more extreme values (outliers) in the distribution.
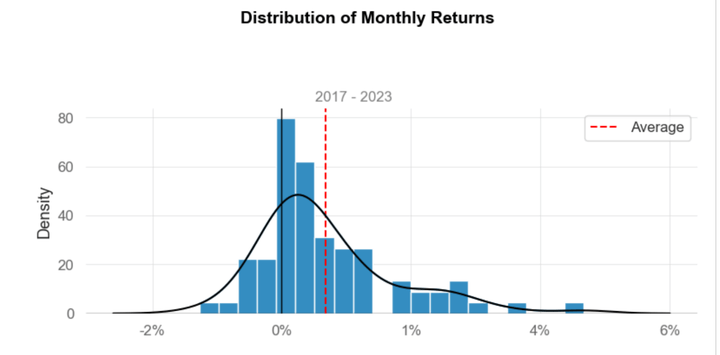
Monthly Returns
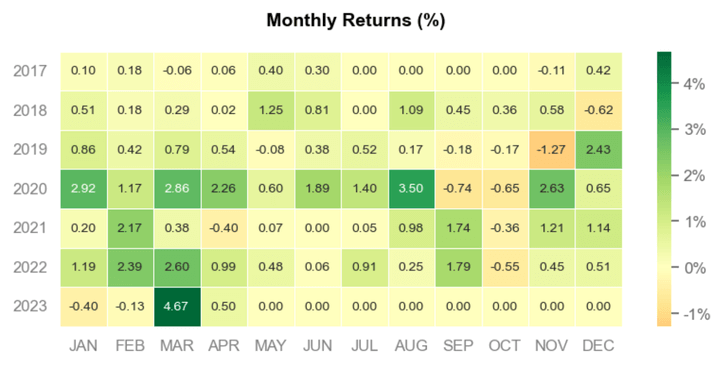
The latter graph of the section shows the monthly returns of the strategy. As we can see, it has performed better in recent years, especially in the last months of this year. This suggests that we can specifically analyse the period of the last two and a half years (i.e. the out-of-sample period).
Out-of-Sample Performance
As introduced above, we now focus on out-of-sample period performance. The difference with the in-sample period is that we estimated the parameters only during the second one (in-sample). In this way, when we back-test the strategy in the last years, we can obtain similar results to those obtained by running the strategy in a real environment.
The out-of-sample return of 22.15% presents even better properties than the overall (in + out sample) return, for example, the Sharpe Ratio of 2.32 (versus the previous value of 2.05) or the Max Drawdown of -2.33% (versus the previous value of -3.07%).
This affirms the effectiveness of such a strategy, at least theoretically. Further work that will be carried out in a subsequent paper will be writing a new operating code to test the strategy in a period of paper trading, to ensure its real profitability.
Conclusion
In conclusion, we can make the following observations: first of all, the strategy can be optimised by making more entries to the market, not only at the thresholds +-2 std, but for example, two entries could be tested at levels +- 1.80 and +-2.25 std and see how the results look. We remind you that all the analyses do not consider transaction and slippage costs, which can be easily added. Finally, we can test the strategy in different periods to see which range to use to estimate the parameters to obtain a better performance.
Frequently Asked Questions
Q1. What is the main objective of this project?
The project tests a cointegrated pairs trading strategy on the 40 largest Italian companies in the FTSE MIB, aiming to exploit market inefficiencies and generate risk-adjusted returns using a mean-reverting framework.
Q2. Why focus on the Italian stock market instead of the U.S. market?
The Italian market is smaller and potentially less efficient than highly developed markets like the U.S., which may create more opportunities for arbitrage and higher adjusted returns.
Q3. What methodology was used to identify tradable pairs?
Pairs were identified using OLS regression to estimate spreads and the ADF test to confirm cointegration. Only pairs with a correlation above 0.8 and stationarity at the 95% confidence level were included.
Q4. How were trade entries and exits determined?
The strategy used Z-score thresholds of ±2.25 as entry signals (long when below –2.25, short when above +2.25). Exits were triggered when the spread reverted to zero.
Q5. How did the strategy perform compared to the benchmark?
From 2017 to 2023, the strategy returned 67.2% vs. 43.1% for the index, with annual volatility of 4%, a Sharpe ratio of 2.05, and a max drawdown of –3.07%.
Q6. What about the out-of-sample performance?
In the out-of-sample period, results improved: 22.15% return, a higher Sharpe ratio of 2.32, and a reduced max drawdown of –2.33%, confirming robustness.
Q7. How did the strategy behave during crises like COVID-19?
During the 2020 pandemic volatility spike, the strategy faced a drawdown but later outperformed, benefiting from the increased correlation between stocks during crises.
Q8. Were transaction costs and slippage considered?
No, the analysis did not include transaction or slippage costs, though these could significantly impact real-world results.
Q9. What are the key limitations of the project?
- Lack of transaction cost modelling.
- Reliance on fixed thresholds (±2.25 std dev).
- Computational simplicity, which could be expanded with dynamic or multi-level entry signals.
Q10. What improvements can be made in the future?
Future work may include:
- Testing multiple entry thresholds (e.g., ±1.80 and ±2.25).
- Incorporating transaction and slippage costs.
- Trying different parameter estimation windows.
- Implementing live or paper trading for real-world validation.
Next steps
If you’d like to go deeper into statistical arbitrage and pairs trading, here are concise resources to guide your build:
Start with the foundations in Statistical Arbitrage (overview), the Statistical Arbitrage glossary, and Pairs Trading Basics.
Move into selection and validation with Selection of Pairs for Statistical Arbitrage and a full walkthrough in Pair Trading Strategy Backtesting using quantstrat.
Explore instrument and market variations: Pairs Trading with ETFs, FX Market Pairs Trading Strategy, Cash Stocks, plus case studies from the Mexican market, Brazil, and Indian market sectors (EPAT project). Browse Algorithmic Trading Projects to shortlist your next build.
For structured, hands-on practice in Statistical Arbitrage, take the Quantra course on Statistical Arbitrage Trading.
Looking for a structured, hands-on path guided by expert practitioners?
EPAT offers a practitioner-led curriculum in Python-based algorithmic trading. You’ll learn core strategies you can adapt to higher-frequency settings, work with broker APIs such as Alpaca, and build mentored live projects. Learn more or register here for our Executive Programme in Algorithmic Trading (EPAT).
Schedule an EPAT counselling call
To understand if EPAT is the right choice for you, talk to one of our specialists who have counselled thousands of learners over the past decade and helped them make the right career decision.
